Star Life Cycle
Studying Stars

Although stars go through a number of changes throughout their lives, most of these changes occur very slowly, over the course of millions or billions of years. This means that astronomers can't simply wait around for them to happen. They have to try and learn about star life in a different way.
The HR Diagram
From Earth, there are a number of things that we can observe about stars. One of the easiest things to measure is the star's brightness, or magnitude. There are a number of things that make stars appear brighter on Earth. One factor is the distance between Earth and the star. Even though our sun is a fairly average star, because it is so close, it appears brighter on Earth than even the brightest objects in the universe. The brightness of a star as seen from earth is called its apparent magnitude. In order to learn more about a star, astronomers usually want to determine its absolute magnitude, or how bright the star actually is.
Another important attribute of stars is their temperature. Astronomers can determine a star's temperature by looking at the color of light that it emits. Hotter stars produce more blue light, while cooler stars produce more red light.
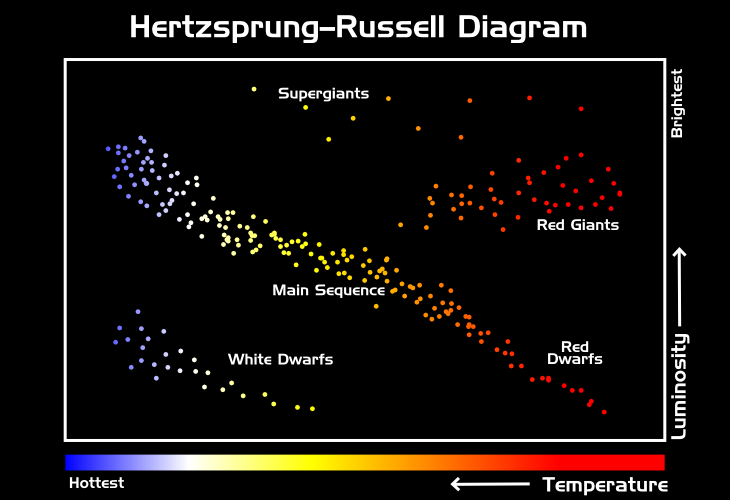
Once astronomers know a star's absolute magnitude and temperature, they can plot it on a chart known as the Hertzsprung–Russell (or HR) diagram. On an HR diagram, the stars at the top are the brightest, while the stars on the bottom are very dim. Unlike most charts, temperature decreases as you move from left to right, which means that the hottest stars are the blue ones on the left, and the coolest stars are the red ones along the right side. By plotting stars on an HR diagram, you can begin to see patterns forming among different stars.
In the following activity, you can help the ASPIRE crew chart various stars on an HR Diagram. As you do so, try to look for patterns and groupings of stars appearing in your data. In what areas of the chart do you get a lot of stars? What parts of the chart have very few stars?
Astronomers now know that these different patterns correspond to different types of stars in different points in their life cycles. As a star ages, its temperature and luminosity will change dramatically, moving it from one category of stars to another. It is important to remember that a star's position on the HR diagram is not related to its position in the sky. Although a star will move around the diagram as it ages, it doesn't actually move around in space.
Mass and Lifespan
Although you might expect bigger stars with more fuel to last longer, the opposite is actually true. The more massive a star is, the faster it burns through it's supply of fuel. A star with 30 or 40 times the mass of our sun will burn brighter, but will only last a fraction of the time that the sun will. Smaller stars, like Red Dwarfs, can last for many billions of years!
Stars and Elements
Most of the matter in the universe is made up of hydrogen, which has just a single proton. In order to get other elements, they must be built out of hydrogen through nuclear fusion, which occurs within stars. Creating new atoms through fusion takes tremendous amounts of heat and pressure to occur, and the bigger the atom, the more energy the reaction requires. Heavy elements, like iron, can only be created in the most massive stars. For heavier elements, even more powerful forces are involved.
This means that the oxygen in the air, the iron in the ground and the carbon in our bodies all were generated in stars that have long since died and scattered their remnants across the universe. If it weren't for these ancient stars, the earth as we know it would not exist.